О коде

Код ANES предназначен для моделирования стационарных и нестационарных пространственно многомерных течений однофазной или двухфазной многокомпонентной сплошной среды в областях сложной геометрической формы, содержащих внутри твердые проницаемые или непроницаемые объекты. В составе кода имеется набор математических моделей и численных алгоритмов для решения широкого класса задач гидродинамики и тепломассообмена.

Главными особенностями кода являются:

код является бесплатным и распространяется под «свободной» BSD-лицензией;
архитектура кода соответствует архитектуре современных коммерческих кодов;
Решатель кода является кросс- платформенным, что позволяет использовать его не только в ОС Windows, но и в многопользовательских версиях ОС Linux;
код позволяет использовать параллельные вычисления на основе MPI интерфейса;
код изначально ориентирован на моделирование процессов в энергетическом оборудовании, поэтому настройка ANES на решение некоторых задач тепломассообмена значительно проще, чем настройки универсальных CFD-кодов.

Базовая математическая модель кода

В расчетной области (РО) могут присутствовать две фазы:

S - фаза: твердые проницаемые или непроницаемые неподвижные конструкции, в общем случае с анизотропными и неоднородными свойствами;
G - фаза: сплошная среда - жидкость или газ, с произвольными теплофизическими свойствами.

Распределение фаз по пространству описывается объемной долей G-фазы, которая в коде называется пористостью - φ. В общем случае РО состоит из набора областей трех типов:

Flow- область, свободная от твердых объектов и содержащая только жидкость ( φ = 1 ),
Struct- область, содержащая непроницаемые конструкции ( φ = 0 ),
Porous- область, содержащая проницаемые конструкции (0 < φ < 1), в которых одновременно присутствуют G- и S- фазы.

Заметим, что:

в расчетной области может присутствовать только S-фаза, состоящая из различных материалов (задачи теплопроводности),
в расчетной области может присутствовать только G-фаза (задачи гидродинамики),
в расчетной области одновременно могут присутствовать S- фаза, состоящая из различных материалов и различные G-фазы.

Типичный пример расчетной области для третьего варианта показан на рисунке 1, где изображена РО для моделирования процессов в металлогидридном аккумуляторе водорода. В этой модели присутствуют два материала G-фазы (водород и охлаждающая вода), несколько материалов непроницаемой S-фазы (сталь, алюминий и медь) и пористые области в которых присутствуют и G-фаза (водород) и S-фаза (пористая засыпка металлогидридного cплава Me).

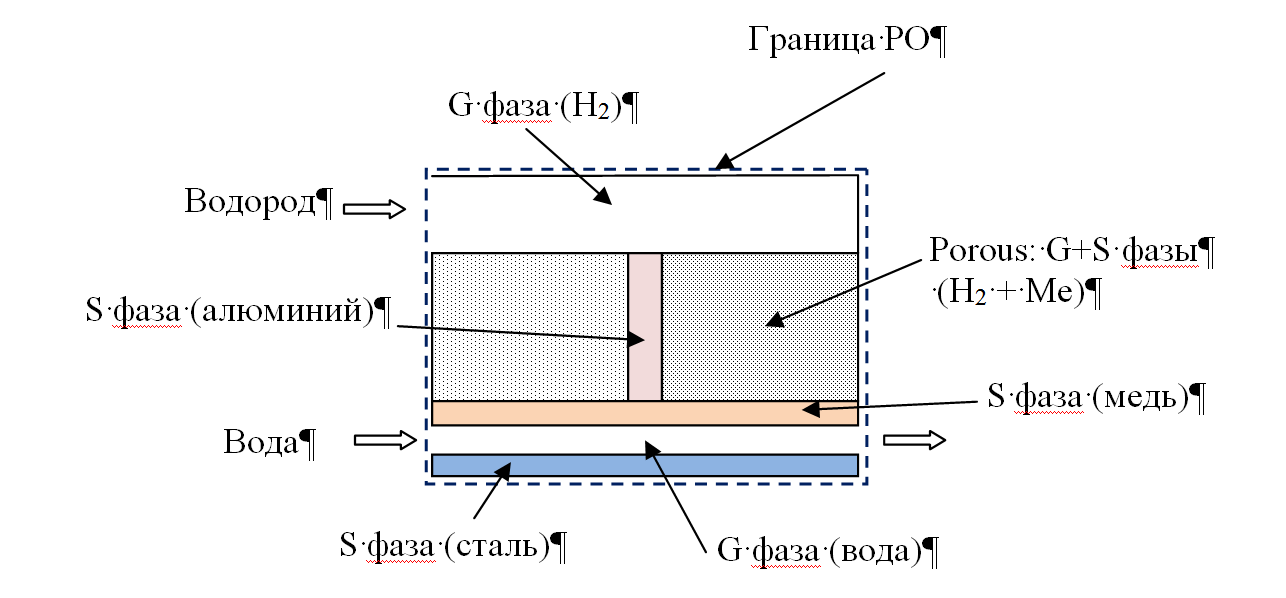Рисунок 1

Основой математических моделей кода ANES является система уравнений переноса для сплошной среды для зависимых переменных Ф:

для G-фазы

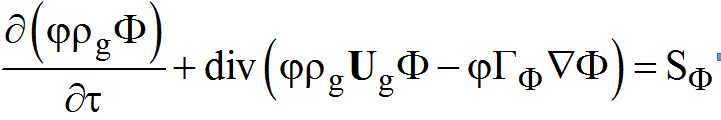
для S-фазы

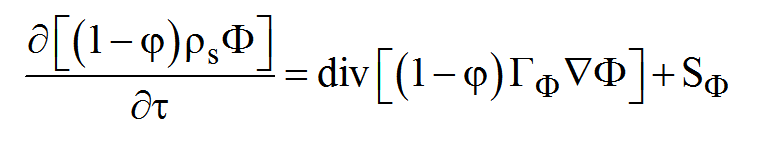
Ф-переменные кода разбиваются на две группы:

предопределенные Ф-переменные (давление, компоненты вектора скорости, энтальпия, массовые доли химических компонентов и т.д.), для которых математические модели реализованы в самом коде,
произвольные Ф-переменные пользователя, конкретный вид уравнений переноса которых полностью определяются пользователем.

Численные алгоритмы кода

В основе численных алгоритмов кода лежит метод контрольного объема (КО). Для решения уравнений гидродинамики (уравнений Навье-Стокса) используются различные модификации алгоритмов SIMPLE и PISO. В частности, в коде реализованы сжимаемые версии этих алгоритмов, что позволяет проводить расчеты:

трансзвуковых и сверхзвуковых течений однофазных сред,
сжимаемых течений двухфазных сред с использованием гомогенной модели потока.

При использовании структурных сеток используется алгоритм SIMPLE для шахматных сеток (компоненты вектора скорости определены в центрах граней КО), при работе с неструктурными сетками используется совмещенные сетки для скоростей и давления (компоненты вектора скорости определены в центрах КО).

Численные алгоритмы поддерживают работу в параллельном режиме. Для этого используется модель декомпозиции расчетной области на подобласти, число которых равно числу используемых процессоров (или ядер). Для реализации параллельных вычислений в коде используется MPI-подсистема. Это позволяет проводить параллельные расчеты не только на кластерах (системы с распределенной памятью), но и на обычных многоядерных компьютерах (системы с общей памятью).

Сетки

Код использует два типа сеток контрольных объемов: структурные и неструктурные сетки в декартовой или цилиндрической системах координат. Для детального описания сложных границ расчетной области в модели неструктурных сеток используется алгоритм дробных ячеек (рис. 2).

В коде Anes реализованы неструктурные сетки специальной структуры, которые называются сетками с локальным дроблением. На этих сетках ячейки имеют форму параллелепипеда в выбранной системе координат (за исключением приграничных ячеек), при этом отношение размера кратны 2ⁿ.

Важной особенностью такой сетки является то, что она представляет собой эффективный компромисс между структурными сетками и полностью неструктурными. Это позволяет с одной стороны работать с сеткой ячеек, используя только два неструктурных списка – ячеек и их граней. С другой стороны, с ячейками можно связать структурные индексы самой мелкой структурной сетки, что существенно ускоряет получение геометрических характеристик ячеек и граней. Другое важное отличие таких сеток от полностью неструктурных – возможность «автоматизации» построения сетки. Для построения такой сетки пользователь должен задать исходную грубую структурную сетку, расположить в расчетной области геометрические объекты, определяющие геометрию расчетной области (РО) и задать максимальный уровень дробления MaxLevel. После этого генератор сетки Компилятора Anes автоматически создаст сетку. Время генерации сетки даже для уровней разбиения 6-8 не превышает нескольких минут, причем это время практически не зависит от сложности геометрии РО.

Важной особенностью кода является то, что он использует собственный генератор сетки, поэтому нет необходимости привлекать сторонние генераторы сеток.

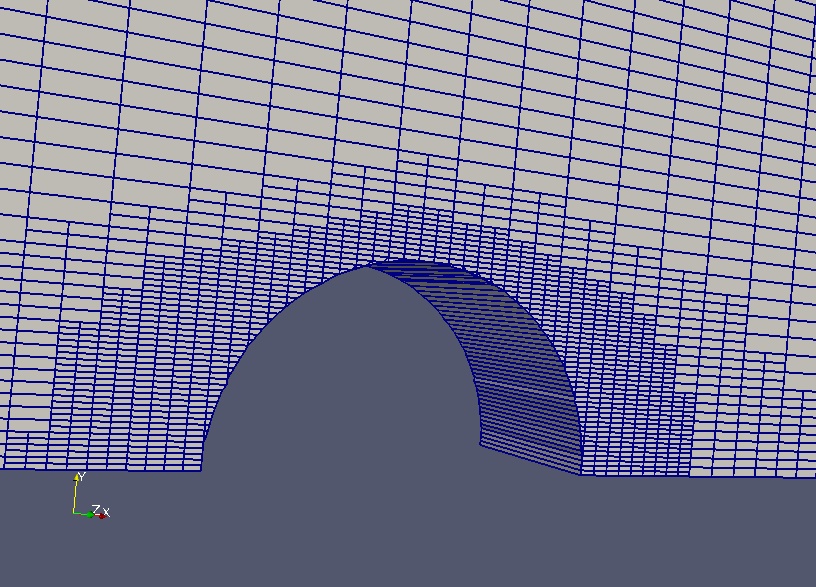
Структурные сетки Неструктурные

Рисунок 2

Математические модели кода

Турбулентность

Для моделирования турбулентных характеристик в коде используется модель турбулентной вязкости. Для ее расчета реализованы следующие модели:

алгебраические модели: LVEL модель Б. Сполдинга и модель Рейхарда,
двухпараметрическая высокорейнольсовская k-ε модель с различными пристенными функциями,
двухпараметрическая низкорейнольсовская двухслойная k-ε модель,
двухпараметрическая k-ω модель c универсальными пристенными функциями Ментера,
SST версия k-ω модели.

Архитектура кода позволяет пользователю легко реализовать как собственные версии алгебраических моделей, так и версии двухпараметрических k-ε и k-ω моделей.

Межфазное G-S взаимодействие

Взаимодействие между G- и S- фазами сводится к обмену массой, импульсом и энергией. Способ описания межфазного взаимодействия зависит от возможности (и необходимости) выделения межфазной поверхности. В коде предусматривается два способа описания межфазного взаимодействия:

1. Пористая модель - в этой модели межфазная поверхность явно не выделяется, обменные источниковые члены в соответствующих дифференциальных уравнениях сохранения носят объемный характер. Эта модель используется для описания G-S взаимодействия в зонах Porous.

2. Модель с явно выделенной границей - в этой модели фазовая поверхность явно выделена и фиксирована в пространстве. Обменные источниковые члены формируются автоматически на основе поверхностных источников межфазного обмена. Эта модель используется для описания G-S взаимодействия на поверхностях раздела Struct и Flow зон.

Двухфазная G-фаза

В коде реализованы несколько моделей двухфазного потока (G-фазы):

Гомогенная модель двухфазного потока с учетом модели сжимаемости G-фазы. В этой модели двухфазный поток рассматривается как однофазная среда с «сильнопеременными» эффективными свойствами, дополненная новой зависимой переменной - массовой долей паровой фазы. Для ее расчета можно использовать либо равновесные термодинамические соотношения (равновесная гомогенная модель), либо уравнение баланса массы паровой фазы с «релаксационным» источником, описывающим метастабильное состояние жидкости (неравновесная модель гомогенного потока).
Модель двухфазного потока с явно выделенной межфазной границей, основанная на использовании VOF-алгоритма. В настоящее время разрабатывается версия, учитывающая массообмен между фазами (испарение, кипение, конденсация).
Лагранжева модель двухфазного дисперсного потока (LDP - Модель). В этой модели для моделирования несущей G-фазы используются однофазные уравнения Навье-Стокса, а для описания дисперсной фазы (частиц или капель) используются лагранжевый траекторный подход. В текущей версии кода реализована первая версия этого алгоритма, основные особенности которой состоят в следующем:

не учитывается влияние частиц на несущую фазу;
отсутствует массообмен и теплообмен между частицами и несущей фазой;
не учитываются процессы распада, столкновения и коагуляции частиц;
все частицы рассматриваются как сферы различных диаметров;
для моделирования взаимодействия частиц с твердыми стенками сепаратора используется упрощенная модель Баи-Госмана.

Гомогенные и гетерогенные химические реакции

G-фаза может представлять из себя гомогенную смесь различных компонент. Для описания состава G-фазы используются массовые доли компонент, которые определяются из решений уравнений сохранения массы компонент. В этих моделях наряду с конвективным и диффузионным механизмом переноса компонента реализованы модели термо- и бародиффузии.

Для моделирования химических гомогенных реакций в самой фазе и гетерогенных реакций на границе раздела G- и S- фаз в коде реализованы специальные математические модели. Пример использования таких моделей - моделирование металлогидридных аккумуляторов водорода - приведен в разделе «Примеры решенных задач».

Модель плавления

В коде реализована модель плавления материалов S-фазы. Ограничение модели - жидкая фаза материала после плавления остается неподвижной и недеформируемой.

Лучистый теплообмен

Если газ не поглощает излучение (оптическая длина для всех частот спектра значительно больше характерных размеров каналов), а сами поверхности можно считать диффузными, то для расчета теплообмена излучением можно использовать модель «Система поверхностей» или S2S модель (Surface – to – Surface модель). В текущей версии кода такая модель реализована для структурных сеток.

Архитектура кода

Код имеет «стандартную» трехуровневую архитектуру: Препроцессор, Решатель и Постпроцессор. Для описания прикладной задачи используется один текстовый файл, который называется файлом проекта пользователя. Для редактирования файла проекта можно использовать либо обычный текстовый редактор, либо диалоговый Препроцессор (рис. 3).

Процесс решения осуществляется двумя консольными программами: Компилятором проекта и Решателем. Главной частью Компилятора проекта является генератор сетки. Модули Компилятора и Решателя являются кросс- платформенными и могут работать в ОС Windows и Linux (рис. 4):

на локальном многоядерном персональном компьютере;
на рабочих многопроцессорных станциях с использованием удаленного многопользовательского режима;
на кластерах в пакетном режиме выполнения задач.

Для анализа результатов расчета можно использовать либо собственный графический постпроцессор, либо универсальный постпроцессор ParaView (рис. 5).

В Компиляторе проекта и Решателе реализован гибкий интерфейс пользователя:

интерпретатор формул в Решателе myForm;
аппарат фортрановских функций для полного доступа к переменным Решателя и настройки своих математических моделей.

Этот интерфейс позволяет описать практически любую прикладную задачу пользователя и легко расширять математические модели кода.

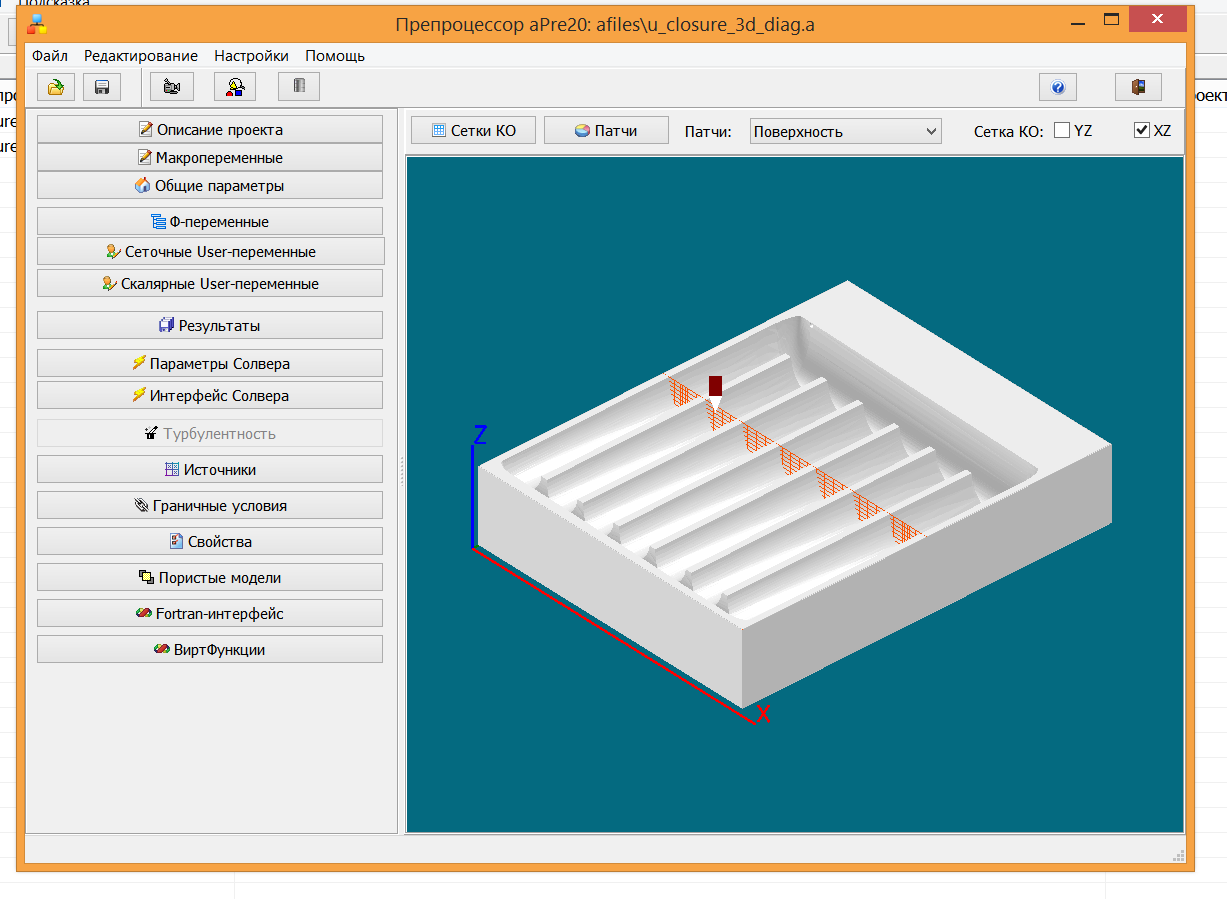
Рисунок 3 - Препроцессор Anes

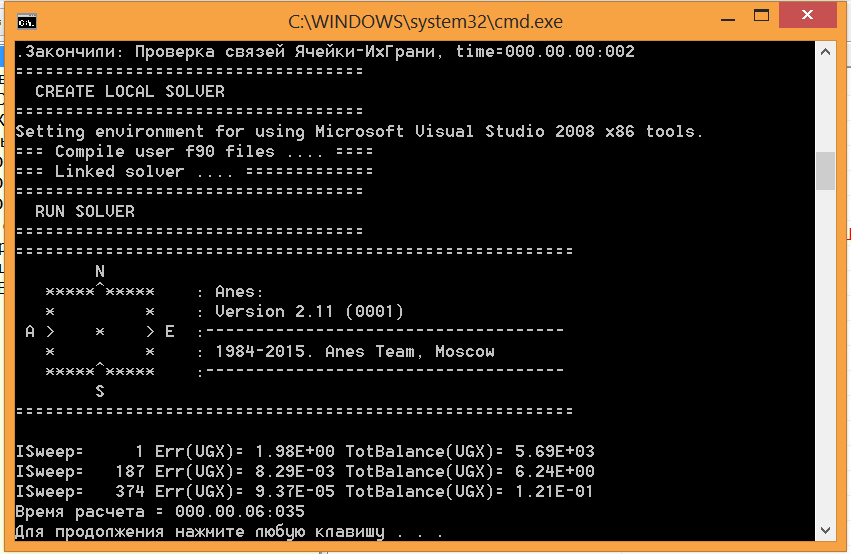
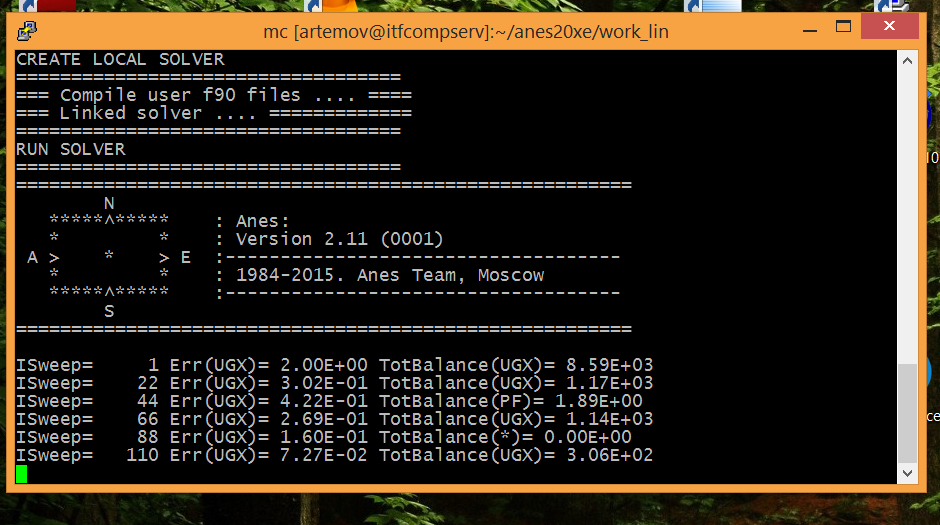
ОС Windows Рабочая станция с ОС Linux

Рисунок 4 - Работа Решателя Anes

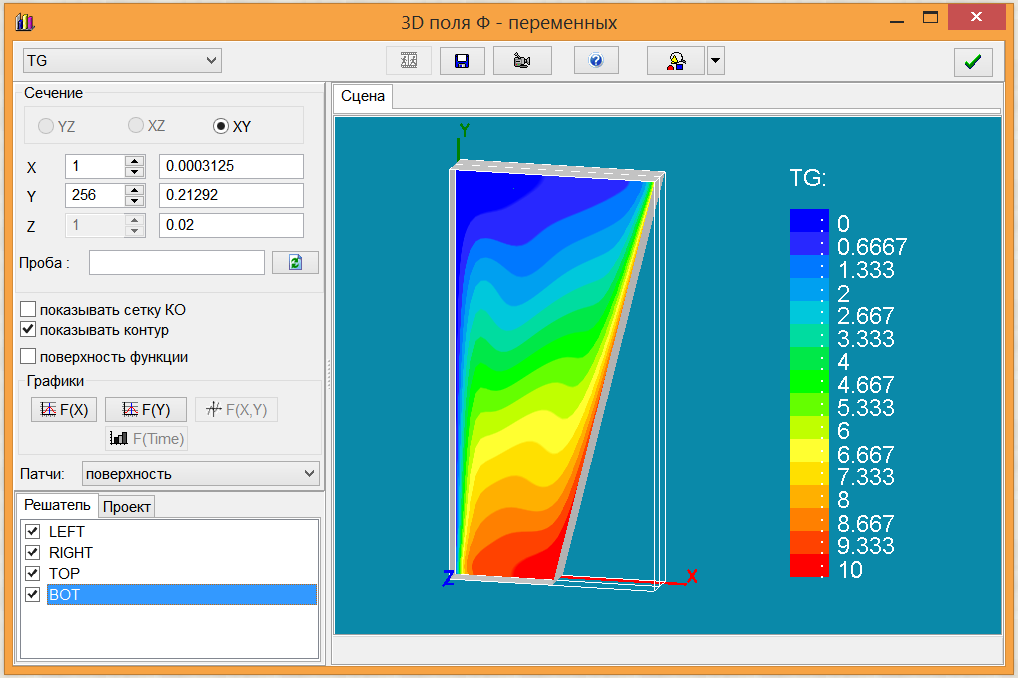
Постпроцессор Anes Постпроцессор ParaView

Рисунок 5 - Анализ результатов расчета